Credo che nessuno di noi abbia mai fatto una considerazione sulla quantità di attività svolta dal nostro cervello nell’arco di una giornata. In maniera del tutto inconscia, i nostri neuroni sono perennemente impegnati a svolgere funzioni che richiederebbero formule matematiche complesse ed avanzate, formule e calcoli che probabilmente non conosciamo e non abbiamo mai studiato in maniera così approfondita.

Ma esattamente quali sono questi calcoli?
Facciamo un piccolo esempio, consideriamo il momento in cui riempiamo un bicchiere d’acqua durante il pranzo.

Nel riempire il bicchiere dobbiamo stare attenti a quanto incliniamo la bottiglia, alla sua altezza ed alla posizione del collo della bottiglia, e nel fare questo non utilizziamo una calcolatrice, ma più semplicemente guardiamo il flusso dell’acqua che entra nel bicchiere e modifichiamo di conseguenza la posizione o la velocità con cui incliniamo la bottiglia.
Possiamo immaginare altre situazioni simili, come quando tracciamo una linea con una penna su un foglio.

Anche in questo caso, decidere quali muscoli muovere ed in che maniera farlo affinché la penna riesca a tracciare una linea diritta, richiederebbe dei calcoli, ma guardando l’effetto sul foglio riusciamo ad ottenere lo stesso risultato.
Possiamo fare infiniti esempi, ed in tutti i casi ci accorgiamo che senza la necessità di alcun calcolo complesso, ma guardando l’effetto causato dal nostro movimento, riusciamo ad ottenere lo stesso risultato che otterremmo calcolando preventivamente lo spostamento della nostra mano.
Di fatto il nostro cervello non esegue alcun calcolo matematico, ma è come se lo facesse perché controlla tutto il corpo, un sistema molto complesso, composto da attuatori, come ad esempio i nostri muscoli, e dei sensori, come i nostri occhi o il nostro udito.
Nel mondo dell’elettronica o della tecnologia, un sistema come il corpo umano viene definito un sistema ad anello chiuso.
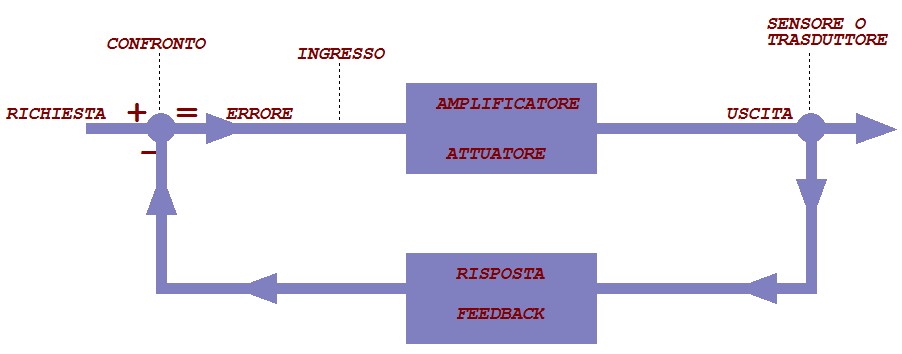
In un sistema ad anello chiuso l’azione compiuta viene rilevata e misurata da un sensore/trasduttore, e l’effetto della nostra azione viene riportato all’ingresso del sistema per correggere il movimento o la generica azione che viene fatta.
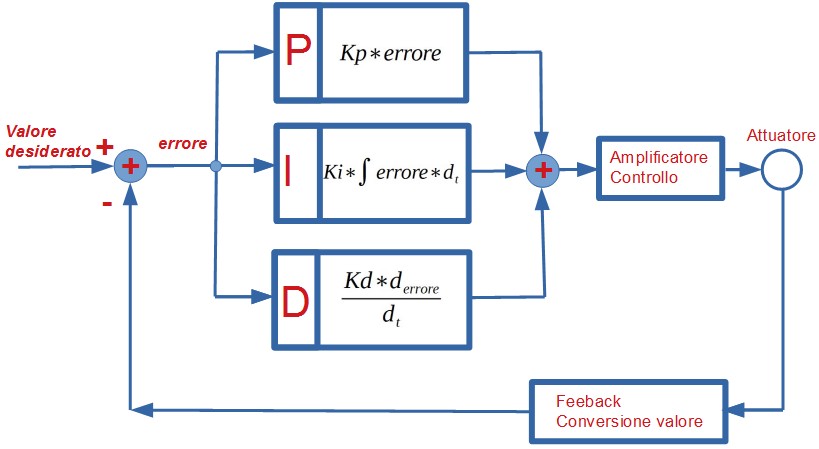
Un sistema come quello di figura, è composto da 4 parti principali:
- L’attuatore, o il dispositivo che compie l’azione, genera l’effetto voluto (un movimento, un suono o altro)
- Il sensore o trasduttore, rileva l’effetto generato,
- Il blocco di feedback, riporta il segnale indietro, eventualmente ridotto, amplificato o convertito,
- Il circuito di confronto all’ingresso, confronta la risposta ricevuta con la richiesta ed esegue l’eventuale correzione.
Proviamo a prendere con la mano una penna posta sul tavolo ad occhi chiusi, sarebbe impossibile farlo, perché il nostro cervello non ha fatto alcun calcolo preventivo (anche se in realtà un ragionamento a monte c’è) e non avendo il feedback del nostro organo sensoriale della vista, non riesce a correggere lo spostamento della mano fino a portarla sulla penna.
Ma se aprissimo gli occhi cosa accadrebbe? In questo caso osservando la posizione della nostra mano che si avvicina alla penna, il cervello riesce a correggere lo spostamento attraverso i muscoli fino a raggiungere l’oggetto.
Anche se a prima vista sembra una cosa facile, vi garantisco che riportare lo stesso ragionamento su un sistema elettronico, richiede diversi calcoli matematici. Ma se vogliamo essere più esatti, dovremmo paragonare il nostro corpo ad un sistema retroazionato con un controllo PID come in figura.
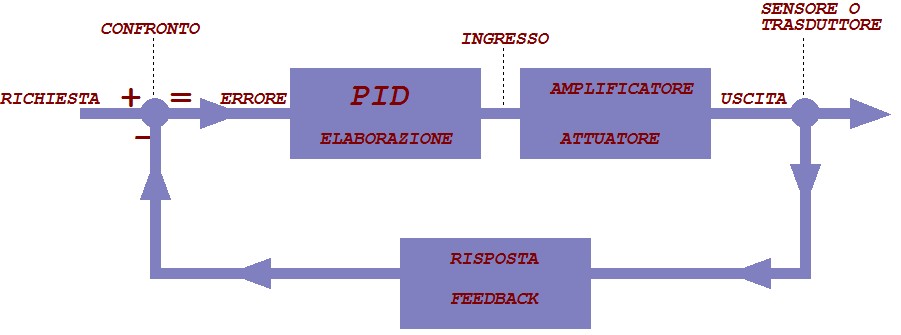
Ma cos’è un controllo PID?
P.I.D. è l’acronimo di Proporzionale, Integrativo e Derivativo . In pratica rappresenta il modo con cui noi correggiamo la nostra richiesta in base all’errore rilevato.
In elettronica questo tipo di controllo viene utilizzato in svariate applicazioni, come ad esempio i dispositivi che controllano la temperatura, (termostati intelligenti) o i controlli numerici per controllare il moto o lo spostamento di un asse motorizzato.
Per comprendere il funzionamento di questo controllo e per vedere se anch’esso viene in un certo qual modo applicato dal nostro cervello, dobbiamo conoscere il significato dei 3 termini che compongono l’acronimo PID.
Come ho già detto in altri articoli, vorrei provare ad utilizzare un metodo comprensibile a tutti, e pertanto cercherò di evitare un approccio prettamente analitico, facendo esempi e ragionamenti accessibili anche a chi non è del settore.
Cominciamo dal primo, il controllo PROPORZIONALE.
Due grandezze si definiscono direttamente proporzionali quando il loro rapporto è definito da una costante K, e pertanto in una rappresentazione grafica, darebbero luogo ad una retta di diversa inclinazione a seconda del valore della costante.

La modifica che nel sistema PID viene introdotta dal termine proporzionale dipende proprio dal valore di questa costante. Facciamo un esempio, consideriamo un sistema che controlla la velocità di un motore per mantenerla costante ad un valore desiderato.
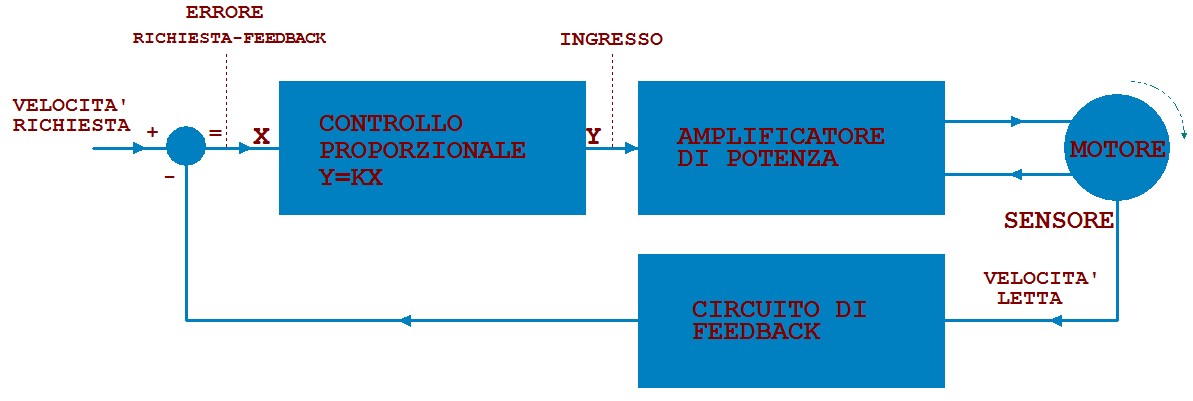
Supponiamo di gestire questo sistema con una tensione elettrica che ha una corrispondenza diretta con la velocità del motore, ad esempio 1 Volt=1000 giri al minuto. A questo valore di tensione (che nello schema abbiamo identificato come “velocità richiesta”) viene sottratto il valore di tensione che si ottiene dal circuito di feedback che tramite un sensore collegato al motore, trasforma la velocità letta in tensione. Il valore ottenuto rappresenta di fatto l’errore commesso tra quanto richiesto e quanto effettuato, questo valore viene poi modificato in maniera proporzionale secondo una costante K e mandato all’ingresso del circuito che si occupa di fornire corrente e tensione al motore (amplificatore di potenza).
In questo caso maggiore sarà l’errore e maggiore sarà la correzione e la successiva azione di controllo.
Variando il valore del coefficiente di proporzionalità K, abbiamo una risposta più o meno incisiva, ad esempio se avessimo K=10 il valore che forniremmo in ingresso all’amplificatore sarebbe più grande rispetto ad un K=2. Ciò significa che aumentando il coefficiente K, abbiamo un aumento o diminuzione della velocità del motore più rapido.
Potrebbe sembrare un metodo sicuro ed efficace per mantenere la velocità del motore costante al valore desiderato, infatti nel caso venga rilevata una diminuzione della velocità, avremmo un aumento del valore in ingresso all’amplificatore e viceversa nel caso di un aumento in uscita, avremmo una riduzione del valore in ingresso. Ma avere solo questo controllo non è sufficiente a garantire una stabilità del sistema, perché ci troveremmo sempre ad inseguire più o meno rapidamente l’eventuale errore. La costante di proporzionalità viene indicata con Kp.
Per quanto possa essere veloce nel correggere l’ingresso, il sistema di accorge dell’errore solo dopo che esso è avvenuto, in quanto il controllo proporzionale lavora sul valore attuale e cioè sul presente e non sul futuro.
Ma è possibile prevedere il futuro o meglio la velocità futura in modo da intervenire prima? Diciamo di si, ed in questo caso entra in gioco il controllo derivativo.
Controllo DERIVATIVO
La situazione comincia a complicarsi, ma come ho già detto, cercherò di descrivere il funzionamento in modo che tutti possano comprenderne il principio. Prima di tutto dobbiamo introdurre un concetto matematico e cioè la derivata.
Consideriamo il grafico visto prima con le 3 rette, in quel caso la variazione di Y è costante, nel senso che ad ogni incremento sull’asse delle X corrisponde lo stesso incremento sull’asse delle Y. Ed in base al coefficiente di proporzionalità abbiamo una differente pendenza della retta. Ricordiamoci inoltre che maggiore è la pendenza e maggiore è la variazione di Y al variare di X.
Ma se l’andamento della grandezza non fosse lineare?
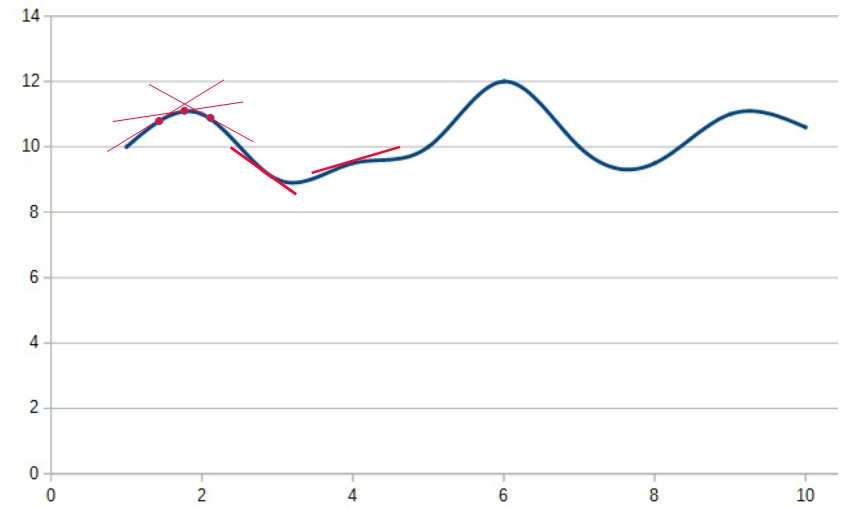
In questo caso non abbiamo una retta, ma infinite rette tangenti ad ogni punto del grafico. La pendenza di queste rette rappresenta la derivata calcolata in ogni punto della curva, cioè la variazione di Y (dY) per ogni infinitesima variazione di X (dX).
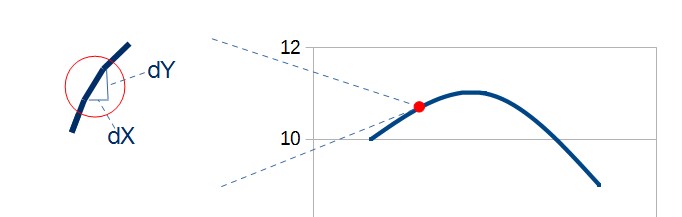
Se sull’asse delle X rappresentassimo il tempo, la derivata rappresenterebbe la velocità con cui il valore di Y cambia.

Nell’esempio precedente del motore, se andassimo a calcolare la derivata del nostro errore, potremmo renderci conto della rapidità con cui esso varia, e conoscere così il successivo andamento.
Per questo il controllo derivativo, ci consente di anticipare le variazioni dell’uscita. Se l’uscita varia lentamente possiamo intervenire in maniera più soft, se invece ci accorgiamo che la derivata aumenta, allora possiamo intervenire e ridurre la velocità in maniera più consistente, andando così a modificare l’ingresso prima che ci sia un concreto incremento del’uscita. Questo ovviamente perché la derivata viene calcolata in maniera veloce e quasi continua, come se andassimo a testare tutti i micro-punti della curva.
Anche in questo caso abbiamo una costante che si chiama Kd e cioè costante derivativa, che è il valore che viene moltiplicato alla derivata per aumentare o diminuire l’effetto di questo controllo.
In questo caso maggiore sarà la velocità con cui varia l’errore e maggiore sarà la correzione e la successiva azione di controllo.
Finora abbiamo guardato il presente, il futuro, ma non abbiamo tenuto conto di cosa è avvenuto in passato. Perché ci può interessare? Beh il passato ci insegna molto, ed avere memoria di ciò che è successo fino ad un determinato momento, ci può aiutare ad intervenire in maniera più intelligente in futuro.
Ad esempio conoscendo il risultato delle nostre correzioni passate, possiamo aumentare o diminuire le correzioni future.
Per valutare ciò che è avvenuto si ricorre al controllo integrativo.
Controllo INTEGRATIVO
Anche in questo caso dobbiamo introdurre un concetto matematico abbastanza complesso che è l’integrale.
Come potete notare non sono stare riportate formule di nessun tipo, in quanto lo scopo è quello di far comprendere il principio di funzionamento di un sistema retroazionato con un controllo PID, cosa che come ho già detto è presente nel nostro cervello senza alcuna necessità di svolgere reali formule matematiche.
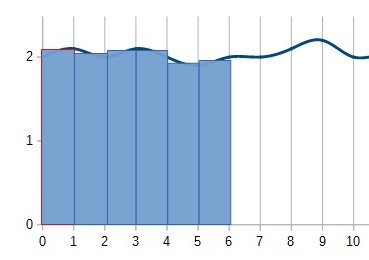
Consideriamo una grandezza (come ad esempio la velocità del motore di prima) oscillante intorno ad un valore. In questo caso avremmo una curva che possiamo ipotizzare come quella del seguente grafico.
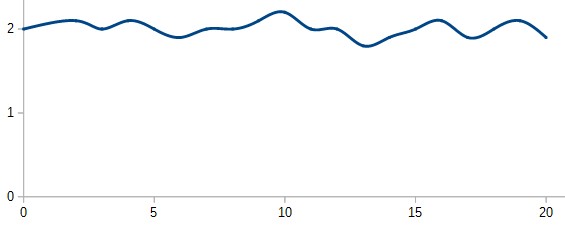
L’integrale definito tra due punti (ad esempio i punti corrispondenti all’intervallo che va da 0 a 1) rappresenta l’area sottesa alla curva.
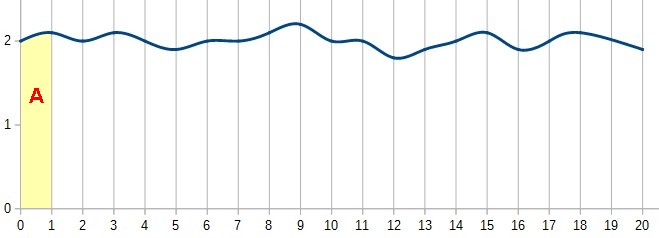
Aumentando l’intervallo l’area ovviamente aumenta.

Il valore di quest’area rappresenta l’andamento del segnale nel tempo, un po’ lo “storico” del segnale, o anche il suo valore medio.
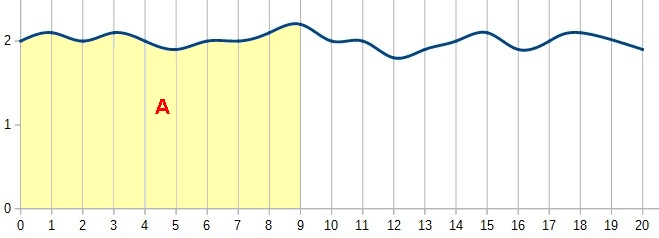
Effettuare la correzione dell’errore considerando il valore medio del segnale o il suo andamento nel tempo percorso, ci consentirà di agire in maniera più intelligente, compensando le repentine variazioni causate anche dagli altri controlli.
Il contributo della componente integrale, è pertanto una correzione proporzionale al valore medio dell’errore.
Per calcolare l’integrale di una funzione (cioè l’area formata con gli asse cartesiani) senza scomodare complesse formule, si possono utilizzare metodi come quello dei rettangoli, graficamente descritto nella seguente immagine, che forniscono un valore approssimativamente valido ai fini del controllo.
Possiamo perciò riassumere quanto detto con la seguente immagine.
Che analiticamente può essere riassunto con la seguente formula.
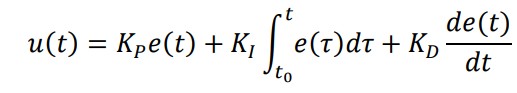
Quanto detto finora è una semplificazione del discorso, che andrebbe approfondito soprattutto dal punto di vista matematico, ci sono in rete diversi documenti utili per comprendere meglio i meccanismi che sono dietro a questo controllo, che nella realtà non prevede solo l’esistenza delle 3 costanti descritte ma di altri valori (ad esempio dei tempi) che possono essere modificati per raggiungere l’obiettivo di un controllo preciso e veloce.
Credo però che un’idea della complessità dei sistemi di controllo utilizzati in elettronica o in automazione ce la possiamo ora avere. Questo tipo di controllo viene applicato in svariati campi, dal controllo della temperatura, della velocità, o di ogni altra grandezza fisica, e questa è un’ulteriore prova di quanto le discipline scientifiche come la matematica, siano dentro ad ogni applicazione tecnologica.
Tornando alla considerazione iniziale, sul comportamento del nostro cervello, lascio a voi valutare quante volte ed in quali occasioni, il vostro cervello utilizza uno o tutti e tre i controlli descritti sopra, se ci ragionate con attenzione, sono sicuro che vi stupirete di sapere che ognuno di noi ha un controllo PID nascosto in un angolo del nostro cervello.
Grazie per l’attenzione.
