Non ce ne rendiamo conto, ma oggi tutte le nuove tecnologie informatiche ed elettroniche, utilizzano numeri, tanti ma davvero tanti numeri. Ogni grandezza rilevata da uno strumento, ogni tecnologia oggi utilizzata è basata sul digitale descritto nel precedente articolo.
Oggi l’elettronica digitale trova spazio in ogni campo, perché in ogni dispositivo elettronico (dal telefonino, all’antifurto alla lavatrice) il controllo del funzionamento è affidato ad un computer.
E’ proprio così, nella lavatrice, nell’antifurto, nella stampante, nella sveglia che abbiamo sul comodino, e in ogni altro dispositivo collegato alla rete elettrica o ad una batteria c’è un computer. Piccolo, più o meno potente, ma comunque un elaboratore con una memoria, un “cervello” che esegue le istruzioni e qualche altro dispositivo per interagire con esso (pulsanti, display ecc….). Sto parlando del microcontrollore che altro non è che un piccolo ed a volte anche potente elaboratore che esegue un programma scritto da qualcuno.

Ma ogni elaboratore che si rispetti deve trattare dei numeri, perciò se consideriamo la macchina fotografica digitale menzionata nel precedente articolo, il suo microcontrollore dovrà occuparsi di memorizzare i numeri che indicano ad esempio la quantità di colore rosso, verde o blu di ogni pixel della foto realizzata.
Non tutti sanno però che i computer come anche i microcontrollori sono dei potentissimi ma stupidi elaboratori. Potenti perché sono molto ma molto veloci (a seconda del loro “clock” un termine che quando acquistiamo un PC ci indica la sua velocità, anche se poi la velocità viene influenzata da tanti altri fattori). Sono stupidi perché riescono solo a comprendere due cifre 0 ed 1, tutti i dati che immettiamo, i caratteri scritti sulla tastiera, le immagini che vediamo i suoni che ascoltiamo, sono un insieme enorme di bit (con questo termine intendiamo la singola cifra che sia 0 o 1).
Forse qualcuno sopra ai 50 anni si ricorda negli anni 70 le schede perforate. Esse erano delle tessere di cartone che contenevano delle colonne forate in posizioni definite, lasciando da parte la codifica delle informazioni, la presenza del foro significa un numero 1 la mancanza del foro il numero 0.
(Cliccando sulla foto si aprirà un sito con il simulatore di schede)
Lo stesso meccanismo è stato utilizzato successivamente nei floppy disk e nell’attuale hard disk, dove il bit viene memorizzato in maniera magnetica su una piccolissima parte del disco, 1 corrisponde alla presenza di una magnetizzazione e 0 all’assenza.
Anche nelle moderne pendrive usb troviamo una memorizzazione per bit in maniera diversa da quella magnetica ma comunque contengono dei bit 0 e 1.
Ma mentre in una scheda perforata era possibile memorizzare credo un centinaio di bit in una pendrive o in una SD card da 16 GB è possibile scrivere oltre a 128 miliardi di bit (0 o 1).
La G infatti sta per giga cioè un miliardo, e la B sta per byte cioè 8 bit, perciò 16 x 8=128 miliardi di bit.
Sembra fantascienza ed infatti se andassimo a vedere con un microscopio dentro alla nostra SD card, rimarremmo esterrefatti nel vedere il grado di miniaturizzazione a cui siamo oggi arrivati.

Torniamo però a noi e cerchiamo di capire come sia possibile con due sole cifre rappresentare tutti i numeri.
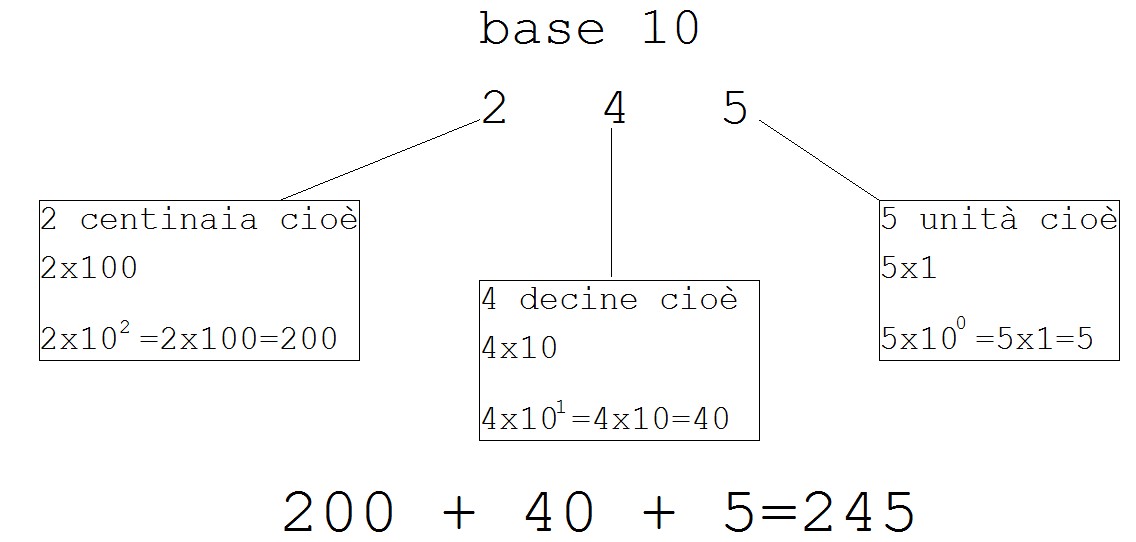
Pensiamo per un attimo al nostro sistema di numerazione decimale che siamo abituati ad utilizzare dalle elementari, se scriviamo il numero 245 intendiamo la somma tra 5 unità, 4 decine ed due centinaia.
Questo perché la base del nostro sistema è 10 (infatti si chiama decimale). In pratica il funzionamento è descritto nella seguente figura, dobbiamo solo ricordare il funzionamento delle potenze dei numeri e che un numero elevato a zero vale sempre 1.
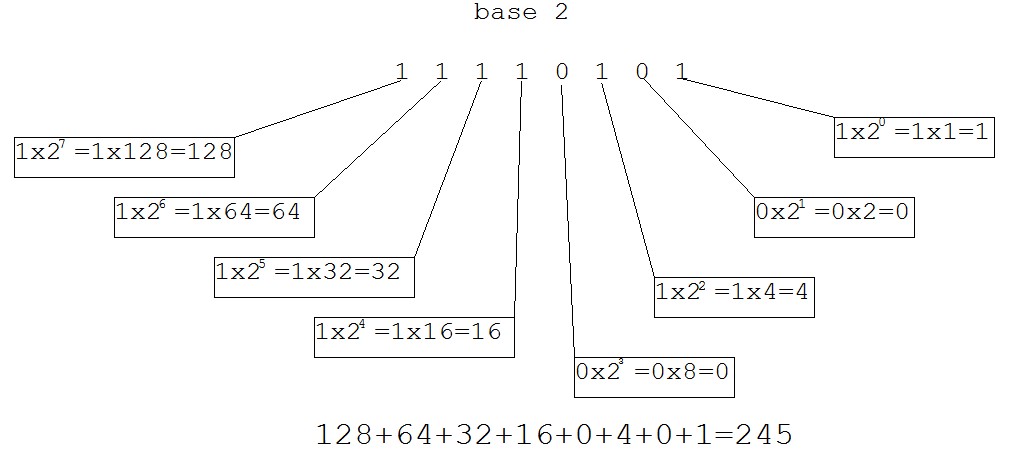
Nel sistema binario il funzionamento è identico con la differenza che la base non è 10 ma 2, perciò lo stesso numero verrà rappresentato dal numero binario 11110101 ed il funzionamento è lo stesso delle unità decine e centinaia con la differenza che essendo la base due dobbiamo moltiplicare per potenze del due e non potenze del 10, perciò ogni cifra che compone il numero, verrà moltiplicata per 2,4,8,16,32 ecc..
Ora proviamo ad immaginare di contare fino a 100 con il nostro sistema decimale, qual’è il meccanismo?
In pratica le 10 cifre che compongono il sistema decimale sono; 0,1,2,3,4,5,6,7,8,9 e con esse componiamo tutti i numeri, quando contiamo elenchiamo le cifre partendo dallo zero fino al 9 e poi aggiungiamo la cifra 1 e ricominciamo da capo, poi arrivati ancora al 9 si aggiunge la seconda cifra e si ricomincia e così via in modo da ottenere quanto segue.

Arrivati a 99 aggiungeremo un altro 1 ricominceremmo daccapo partendo perciò da 100…..
Questo è un meccanismo che conosciamo benissimo, e possiamo applicarlo anche ad un sistema in base 8 che però ha solo 8 cifre 0,1,2,3,4,5,6,7. In questo caso otterremmo:

E con un sistema binario? In questo caso abbiamo solo due cifre perciò avremmo:

Andando a confrontare il conteggio del sistema decimale con quello binario avremmo la corrispondenza tra i due:

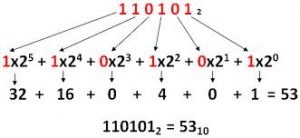
Se vogliamo verificare la corrispondenza tra i numeri, potremmo provare a convertire il numero binario in decimale come abbiamo fatto prima ricordandoci il seguente funzionamento.
Inoltre con il sistema binario potremmo rappresentare anche i numeri negativi utilizzando il bit più a sinistra (chiamato MSB, Most Significant Bit e cioè bit più significativo) come segno, se è 1 il numero composto dagli altri bit è negativo.
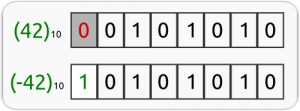
In questo caso stiamo parlando di numeri interi, ma con il sistema binario possiamo rappresentare anche numeri con la virgola, ad esempio con un particolare metodo con soli 4 byte (32 bit) si possono rappresentare numeri che hanno la seguente estensione:

Aumentando il numero di bit potremmo andare ancora oltre.
In pratica con il sistema binario, come con gli altri sistemi, si possono rappresentare tutti i numeri reali possibili e non solo, infatti utilizzando il sistema binario possiamo anche rappresentare caratteri alfanumerici e simboli, basta cercare su google “codice ASCII” e verranno fuori tante tabelle dove ad ogni carattere (numero, lettera o simbolo) viene associato il corrispondente numero in binario. Ad esempio secondo il codice ASCII quando scriviamo una lettera dell’alfabeto nel nostro computer viene memorizzato il corrispondente numero in binario secondo la seguente tabella.

Tornando all’immagine fotografata con la nostra macchina digitale, dobbiamo immaginarla composta da miliardi di cifre 0 ed 1, che rappresentano i colori di ogni pixel e tutte le altre informazioni (contrasto, luminosità ecc…) che compongono la nostra foto.
L’esponenziale e rapida crescita del digitale, è avvenuta perché riusciamo oggi a memorizzare diversi miliardi di bit in poco spazio, potendo perciò memorizzare qualsiasi cosa; immagine, video o canzone, senza perdere in qualità. Inoltre essendo tutto convertito in numeri, è tutto modificabile o velocemente duplicabile per essere memorizzato nei vari supporti oggi disponibili (DVD, SDcard, pendrive, ecc….) chi ha oltre i 40 anni sa benissimo che per duplicare una musicassetta o un disco in vinile, occorreva praticamente ascoltarlo per intero, mentre oggi con pochi secondi riusciamo a spostare centinaia di canzoni dal PC alla nostra pendrive.
Come descritto nel primo articolo ho cercato di rendere comprensibile questi argomenti a chi non è del settore e non ha alcuna conoscenza tecnica, spero davvero di esserci riuscito, in caso contrario non esitate a commentare con dubbi e domande, risponderò appena possibile.
Scriverò anche articoli o tutorial per gli “addetti ai lavori”, dove certe conoscenze dovranno essere date per acquisite, in quel caso cercherò comunque di essere esaustivo e di utilizzare un linguaggio tecnico per quanto possibile comprensibile a tutti.
Grazie.

